Youtubeで英語学習
Youtubeで「TED」の動画を見て英語を勉強されている方も多いと思います。
本記事では、Youtubeの字幕機能で字幕を書き起こして、さらに日本語に翻訳してみます。

Youtubeでの字幕表示方法(字幕が微妙な時もありますが、無いよりはずいぶんマシ)
Mathematics and sex | Clio Cresswell TEDxSydney
(出展:TEDxSydney)
結婚や恋愛に関する方程式を紹介する女性数学者の講演です。
個人的に「数学」と聞くと退屈なものという印象しかありませんが、
- 容姿端麗な女性数学者というギャップ
- 聴衆と一体感のある講演
- 講演者の数学への情熱
これらがあいまって、飽きさせない内容となっています。
1.結婚が長続きするかどうかを表した方程式
Yes, I’m a mathematitian who is goning to get you so laid.
(laughter)
私は数学者ですが、これから皆さんとたくさんエッチな事をします。
(会場笑)
And, uh, to begin, I need you to stare at this equation.
I mean, there’s your first orgasm right there, I know it.
始めに、皆さんこの方程式を見てください。
ここで皆さんは最初の絶頂を迎えることでしょう。

But these are very sophisticated equations that model a successful marriage.
And they are groundbreaking equations because it was the first time that truly sophisticated mathematics was used in the field of romance.
さて、これは非常によくできた方程式で、実りある結婚を図式化したものです。
そして、これまでに無い方程式でもあります。なぜなら、ロマンスの領域において初めて用いられた方程式だからです。
And they predict with 95 percent acuracy rate whether newlyweds will be together in 6 years time.
And you can see there’s the “W” for wife, and the “H” for husband.
この方程式は95%の確率で、新婚さんが6年後にまだ離婚していないかを予測する事ができます。
「W」という変数は妻の事、「H」は夫の事です。
So, they modeled newlyweds talking about areas of contention like the in-laws and money.
And then they modeled the responses according to how each partner was responding to the other.
Body language as well.
義理の両親やお金など、議論の的になる領域を新婚夫婦が話す事に関して、図式化しています。
更に、お互いがどのように反応するかについても数式化しています。
もちろん、ボディー・ランゲージも含んでいます。
(1:00)
And what came out was this interesting influence factor at the end there,
which actually revealed the couples that responded the least to each other had a better chance of successful marriage.
So that means,
(laughter)
分かった事は、この興味深い影響力の要素です。
互いに対する反応が最も控えめな夫婦ほど、結婚が長く続くという事実です。
つまり、
(会場笑)
I see some people are like
“Poof, we knew that.”
So, couples that compromised the least ended up being together the most.
皆さんのうち何人かは、
「ふん、そんなの知ってたよ。」
という反応をしていますね。
夫婦喧嘩が少ない夫婦ほど、一緒に居続ける事が多いです。
And this was very interesting because a lot of therapy has been based on empathy.
And you laughed before, so maybe you don’t say when your partner comes home,
“Yes darling, I know. Let me rub your feet and fix you a martini.”
Because what they’ve actually found is that might not be the best way forward.
これは非常に興味深い事です。なぜなら、多くのセラピーが共感に基づいているからです。
皆さんが先ほど笑ったように、たぶん皆さんは結婚相手が帰宅した時に、
「あなた、足のマッサージをしてあげるわ。マティーニを作ってあげる。」
なんて事は言わないでしょう。
なぜなら、このようなやり方は将来への最善の方法ではない、と確認されているからです。
Maybe the best way, or the mathematics revealed,
that having high standards and finding ways to reach for those standards is in fact the way to go.
おそらく最善の方法にたどり着くには、または数学が発見したのは、実際まだ多くの道のりがあるという事です。
2.数学の革命:「軽めの科学」
So the mathematics is all the study of patterns.
All the symbols that you see are in the fact patterns.
You know, encapsulating patterns.
数学は全て、パターンの研究です。
数学で目にする記号は、現実に起きる事の類型化です。
暗号化のためのパターンです。
(2:00)
And we’re very used to seeing mathematics being used in physics, engineering.
That’s just because it’s been there the most.
You know, E equals mc squared.
That’s so early 1900’s.
一般的に、数学とは物理学や機械工学で用いられるものだと考える傾向があります。
もちろん、それらの領域で最も多く数学が使われてきたからです。
例えば、E=mc2乗.
ただし、それは19世紀前半の話です。
There’s actually been an evolution.
Since the 80’s we have seen mathematics venture into stock market analysis, risk analysis that was new.
And then since the 90’s or 00’s even we’re seeing mathematics enter into the sometimes called Softer Sciences,
like psycology, sociology, anthropology, biology.
実のところ、数学には革命がありました。
80年代から、数学は証券市場の分析に用いられたり、リスク分析に用いられるようになりました。
90年代や00年代には、「軽めの科学」と呼ばれる領域でも数学は用いられ始めました。
「軽めの科学」とは、心理学、社会学、人類学、生物学などの事です。
And, uh, new mathematics appears everyday.
I brought in a few just to remind you of how that works.
新しい数学は毎日生まれています。
皆さんにいくつかお見せしようと思って持ってきました。
So, here’s some latest research.
This is looking at antibiotic use and how to implement antibiotics for tuberculosis while getting the patient health,
making sure to avoid antibiotic resistance.
And that came out a couple of weeks ago.
ここで採りあげるのは、いくつかの最新の研究です。
これは、結核に対して抗生剤を使用する際、患者を健康に保ちながら、抗生剤の副作用を抑えるにはどうすればよいかを示しています。
数週間前に発表されたものです。
And this is looking at how opinions spreads through a population.
And when you have co-existense of several opinions or one big consensus.
これは、人々の意見がどのようにして多くの人に拡散するのかを示したものです。
複数の意見の共存や、意見の一致が示されています。

One of my favorites, it’s older but I couldn’t resist.
This one is from 2009 and this is how to create a perfect chocolate.
One that melts in your mouth but not in your hand.
And yes, these are very sexy equations, I’m sure you’ll agree.
私の一番好きな数式の一つです。ちょっと古いですが、我慢できないので出してしまいました。
2009年に発表されたもので、完璧なチョコレートを作るための数式です。
口で溶けて、手では溶けないチョコレートです。
そうです、これらはとても魅力的な方程式です。皆さんそう思うでしょ?
3.愛の方程式
(3:00)
So, mathematics is absolutely everywhere these days,
it’s used everywhere, so it really is no surprise.
that now we’re seeing the equations for love.
さて、数学はいまや至る所に存在しています。
だから今さら驚きませんね。
ここで愛に関する方程式の登場です。
Now, love sucks.
I know you all know that.
Because, yes, you’re excited at first.
But then you’re scared.
Oh, my god. I haven’t eaten.
You’re sitting looking at your phone, “Please ring!”
Then they send you two-text word and you’re like “Whoo-hoo! It’s on like Donkey Kong.”
(laughter)
さて、愛とは厄介なものです。
たぶん皆さんも経験済でしょう。
初めの方はとても盛り上がります。
でもそのあと、怖くなります。
ああ、困った。ご飯がのどを通らない。
じっと座って電話を見つめながら、「頼むから鳴って!」
そしてたった二言のメッセージが届いただけで、「やった!これで彼とうまくいく!」と喜んでしまいます。
(会場笑)
And these equations look at which personality traits are more likely to come together
to have a more stable companionship type love
because some people just end up being up and down continuously.
この方程式は、どんな個人的特徴を持つ人たちがちゃんとしたお付き合いに発展するかを調べたものです。
なぜなら、中には落ち込んだり盛り上がったりを繰り返すだけの人々もいるからです。
Imagine being in a relationship with Charlie Sheen.
That would be like well, unlike Donkey Kong.
and also like this
(laughter)
チャーリー・シーンと付き合ったと考えてみてください。
とても安心してなんていられないですよね、ドンキーコングとは違って。
(会場笑)
(4:00)
It gets a bit out of control mathematically quite fast.
So just to tell you, it’s about one thing to look out for is if your partner,
If you overestimate partner’s quality so with partners we can behave a bit like proud parents.
“He’s so smart, He’s so sexy.”
Everyone’s just staring at this guy like —
Anyway,
(laughter)
数学的に、感情をコントロールできなくなるのは時間の問題です。
だから言っておきます。
もし、相手の事を過大評価してしまうと、私たちは親バカの親みたいになってしまいます。
「彼はとても頭がいいの。それにセクシーなの。
他の人はみんな彼を見つめるの」
(会場笑)
4.男性の性体験の数は女性の4倍?
Here’s some more mathematics.
Now, men report, on average, having had sex with 2 to 4 times as many women than women do men.
And this doesn’t make sense.
It doesn’t.
(laughter)
もう少し数式をお見せします。
さて、調査によると、女性の性体験の数と比較して、男性はその2倍から4倍の性体験をするそうです。
これは計算が合いません。
全然合いません。
(会場笑)
I know you’re all thinking, “But what about prostitutes?”
“What about my ex? He slept with everybody.”
No, every time a man has sex with a woman there are averages for others things.
But in a large enough sample space, it’s gonna be about the same, not off like this.
皆さんこう考えているのではないでしょうか。「売春婦は勘定に入れた?」
「私の元カレは?アイツは誰とでも寝てるわ。」
違います。男性が女性とセックスする時、そこには他の物事と同様に、平均値と言うものが存在します。
サンプル数が充分に大きくなると、平均値はこんなに違ったりはしません。
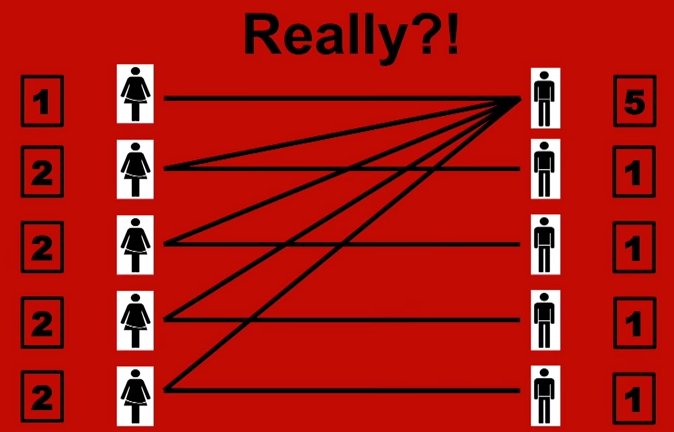
So here’s an example.
He is Charlie Sheen.
He’s had sex with everyone.
Then the nexy guy, only one, one, one, one.
さて、ここで例を挙げてみましょう。
右上の男性はチャーリー・シーンです。
彼は全部の女性とセックスしました。
次の男性は、一人だけ、一人、一人、一人。
(5:00)
That forces, you see, the outcome for the women.
The first one’s had one, the others have had 2 partners each.
and 2, 4, 6, 8, 9.
9 diveded by 5
これで自然と、女性の結果も出ます。
最初の女性は一人だけ。他の女性は二人。
二人、四人、六人、八人、九人。
9割る5。(=1.8)
and on the right 5, 6, 7, 8, 9.
9 devided by 5.
右側も、五人、六人、七人、八人、九人。
9割る5。(=1.8)
Every time a man has a sex with a woman.
It’s adding to the general tally of both sides.
男性が女性とセックスした時、
同じ数が男性と女性に足されます。
Now, why is this discrepancy?
Because the surveys are confidential and non-identifying,
it turns out, if you ask about kinky things, people are very honest.
さて、なんで女性と男性で性体験の数に食い違いが起きるのでしょうか?
調査が信頼がおけるもので、匿名性がある場合、
イヤラシイ質問をしても人々は正直に答えてくれます。
So what we’ve turned to is we think it’s counting strategy.
Because if you enumerate you’ll be prone to an underestimation.
If you approximate you’ll be prone to an overestimation.
このような場合、集計の戦略を当てはめます。
一つ一つを数えあげる場合、人々は過小評価する傾向があります。
しかし、だいたいの数を答える場合は、過大評価する傾向があります。
So it seems women are going, “Justin, Brad, the guy with the sexy biceps. The end.”
And men are going, “20 a year for the last 5 years.”
You know.
(laughters)
女性たちは、「ジャスティンでしょ、ブラッドでしょ、二の腕がセクシーなあの人でしょ。終わり。」
男性たちは、「ここ5年では、一年あたり20人だな。」
こんな感じでしょう。
(会場笑)
(6:00)
My favorite clue in all the data was that 80 percent of men’s results were divisible by 5.
So, of course the mathematicians are like,
“Yeah, no, you’re lying.”
(laughter)
80%の男性の回答は、5で割り切れる数だというのが、私のこの仮説の根拠の一つです。
だから、もちろん数学者たちは、
「ああ、君は嘘ついてるね。」
と思っています。
(会場笑)
5.女性ホルモンと男性ホルモンの方程式
Back to some more waves.
Of course, there are waves in women’s hormones.
And these equations look at what kind of mechanism is in a woman’s body.
how does your body know 28 days have gone by?
いくつかの変動に戻ってみましょう。
もちろん、女性ホルモンにも変動があります。
そしてこの方程式は、女性の体の機能についてのものです。
どのようにしてあなたの体は28日過ぎた事を知ることができるのでしょう?
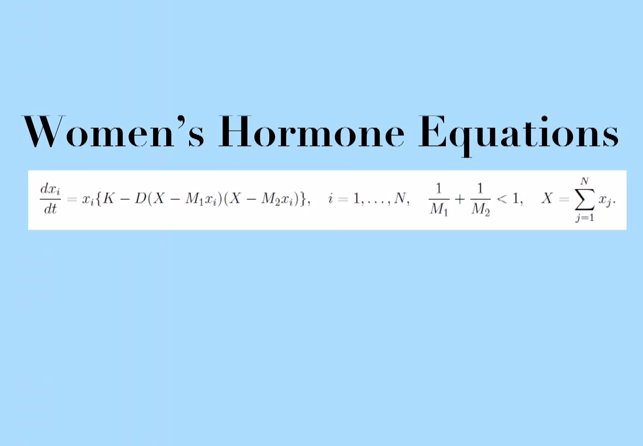
And it’s based on understanding why women have all their immature eggs at birth ready to go.
We hear so much about women’s hormones,
so I’ve brought in men’s as well.
これは、なぜ女性が未成熟な卵子を抱えて生まれてくるのかについての理由に基づいています。
女性ホルモンについてはとてもたくさんの事を私たちは知っています。
そこで、男性ホルモンについての方程式も見てみましょう。

These are (laughter)
These are real, I’m not making them up.
These model the relationship between the brain and the testes as the fluctuation happens during the day.
これらは(会場笑)
これらは本当なんです。勝手に作ったわけじゃないんです。
このモデルは脳とテストステロンの関係についてのもので、一日の間に起きる変化を説明しています。
(7:00)
I promise these are real.
Testosterone, for example, has a peak in the morning.
And a slump in the evening.
But there’s actually a mini testosterone peak every 2 to 2.5 hours in between.
本物の方程式なんですよ、約束します。
テストステロンは、例えば、朝にピークを迎えます。
夜には不調になります。
でも実際は、小さなピークが2時間または2.5時間ごとに訪れます。
So, you know what that means.
Especially women.
If you ask a guy a favor and he’s not responding just wait half an hour and ask again, just try and
(laughter)
just try and get that slump moment.
It’s got its purposes.
Though the peak has another purpose as well.
何を言いたいか分かりますよね。
特に女性の皆さん。
もしあなたが男性にお願いをして、彼の反応が悪かったとしても、30分待ってから頼んでみてください。
(会場笑)
不調のタイミングを探ってみてください。
目的に適っています。
ピークはもう一つの目的を持っています。
6.セックスについて考えると頭が良くなる
Yes, this is all great fun and I could carry on with fun maths.
and sex problems for hours.
But ultimately, what I’m about is our amazing brain.
and the impact of abstract thinking and the power of abstract thinking.
この話はとても楽しくて、まだまだ続きます。
数学とセックスに関してなら何時間でも話せます。
でも最後に、私たちの素晴らしい脳の話に進みたいと思います。
抽象的な思考の持つ力についてです。
(8:00)
And so let me turn things a little bit around you and say,
What do you think happens if you think about sex before doing mathematcs?
Because it’s actually not super distracting.
数学の前に、セックスに関して考えると何が起こると思いますか?
それは実のところ、集中力の妨げになるわけではありません。
You’ll actually become better at doing certain types of brain processes.
It turns out there’s 2 fundamental types of brain processes.
You either think globally or locally.
Forest or trees.
実際、ある種の脳の機能を向上させることになります。
脳には二つの基本的な機能があると分かっています。
それは、グローバルな思考と、ローカルな思考です。
森と木、ですね。
And when you’re solving a problem,
you often start with the global kind of analysis
and you have to dig in deep and follow leads to solutions.
問題を解いている時、
ふつうはグローバルな分析から入ります。
そして、深く掘り下げていって、解決への糸をたどっていきます。
And it turns out that we’re now seeing with the latest research
that this is linked to creative versus anylytical thinking.
And more than that we’re finding that it’s actually very easily manipulated.
最新の研究では、
創造的思考と分析的思考のつながりが分かっています。
それ以上に、これらの思考は容易に操作する事ができると分かりました。
So if you get people to think about love and then solve problems
they’ll be better at the globalization, the beginning, the creative part.
And if you get people to think about sex,
they get better at process part of the problem solving.
Easy as that.
だから、人々に愛について考えてから問題を解いてもらうと、
グローバルな思考とクリエイティブな思考、両方が強化されるのです。
問題解決の処理能力が向上するのです。
こんなにも簡単に。
7.「数学」とは何か?
And here’s the bigger question that interests me.
What is this thing called mathematics that’s only been going for about 2,000 years that popped up independently across the world
that so many people swear they can’t do?
私を惹きつけてやまない、もっと大きな疑問があります。
この2000年の間に突如として世界に現れて、多くの人々が「ムリだ」と諦めていた問題を解決した、数学と呼ばれるものは一体何なのだろう?
(9:00)
See, there’s something that’s not quite reconciling there.
You can’t have something that’s developed so recently with some people just having an extra brain bit.
No, that doesn’t make sense.
It’s about finding those right triggers.
説明のつかない何かがそこにはあります。
数人の頭がいい人たちがいたからといって、いきなりこんなものを手に入れる事はできません。
まったく説明ができません。
正しいきっかけを見つけるにはどうしたらいいでしょうか。
Here’s a school report card of mine, in French,
My parents are these wild, wild travelers always looking for wild parties.
I’m actually the conservative offspring of some crazy wild people.
これは私の学校の成績表です。フランス語ですね。
私の両親はおかしなおかしな旅行好きで、いつも楽しい場所を探していました。
私は、実はそのような変な人たちから生まれた、保守的な人間なのです。
And, as you see, we lived in Cannes, whatever.
Great parties there.
But more importantly, you can see 2 out of 20 for mathematics.
And my best result was 15 for Travaux Manuels et Technique, which is woodwork.
(laughter)
ごらんのとおり、私たちはカンヌに住んでいました。
楽しいところでしたよ。
重要なのは、数学の欄に「2」という数字を見ることができるでしょう。
これは、20点満点中の「2」です。
私の最高点は「15点」、トラボー・マヌエル・エ・テクニークで、それは木材工作の事です。
(会場笑)
So it’s very clear to me what life is like without mathematics.
Once I found mathematics at 18 when I came to Australia,
it was the first time that I was connecting to something pure, to something that was so amazing.
そう、私にとって人生とは数学と無関係なものだという事は非常に明らかでした。
18歳でオーストラリアに来て数学の魅力に気付くまでは。
それは私にとって初めての事でした。純粋で、とても魅力的なものにつながる事ができたのです。
8.野生動物と「数学」の関係
(10:00)
You see, pattern recognition is right at the core of the animal kingdom.
You see, even reptiles recognize whether it’s something to eat, fight or have sex with.
and, even a jellyfish knows which way is up and which way is down.
パターン認識は、野生生物の世界においては根幹となるものです。
爬虫類は、食べ物、敵、繁殖相手を区別できます。
クラゲでさえも、どちらの方向が上なのか下なのか、知る事ができます。
Now the seeds of the number concept are also very much part of the animal kingdom.
A pack of animals will recognize whether another pack is greater than theirs.
and you can actually teach a rat to press a lever an approximate number of times to get food.
数字の概念の基礎は、野生動物の世界でも存在しています。
動物の群れは、別の群れの数が自分たちより多いかどうかを判断しています。
またネズミに、食べ物を手に入れるために大まかな回数、レバーを押すように教える事もできます。
Now, you see how I the word approximate.
That’s because the rat doesn’t have self-awareness or a linguistic ability to capture tame those innate sensations.
So if the rat is just tapping 3 times 1, 2, 3 – it will kind of get it right.
But once it gets to 16, the poor little rat is tapping away it doesn’t know where it’s reaching.
ここで、「大まかな」と私が言った事に気付きましたか?
ネズミは、生まれつきの感覚を活かすための、知覚能力や言語的能力を持ち合わせていないからです。
よって、もしネズミが3回だけ叩く事を覚えるのであれば、それはだいたいうまく行きます。
しかしこの数が16になると、かわいそうな小さなネズミは、覚える事ができません。
(11:00)
And it’s the same with us.
If you do an experiment where we can’t count out we’ll make exactly the same mistake as the rat.
これは、私たちも同様です。
もし、数を数えることができない条件で実験を行えば、私たちもネズミとまったく同じ過ちを犯します。
Now, we went further.
We went to things like 2 + 5 = 5 + 2.
I can swap the order of things and still reach the same result.
幸いなことに、私たちは先へ進むことができました。
2+5=5+2のようなものへたどり着きました。
数値の順番を変えても、同じ結果が得られます。
We went further still.
A + B = B + A
I can substitute any of the infinite number of numbers that I’m now aware of in that formula and it means the same thing.
人類はさらに先へと進みました。
A+B=B+A
この中の変数をどんな数字に変えても、全く同じ事を意味する公式です。
You see, language is more that just naming things.
With it, we also got cause and effect and temporal reasoning.
お分かりでしょうか、言語には単に「物に名前を付ける事」以上の役割があります。
言語があれば、私たちは原因と結果、一時的な理由づけを知ることができます。
And you see, mathematics is our most precise use of thinking syntactical understanding.
Because with mathematics at each step that you’re creating the pattern linking discovery, there’s no ambiguity.
It is very precise what you’re doing at each step, what is in each classification.
True or false. That’s it.
数学とは文章を用いて世界を理解するための最も正確な利用法です。
数学を用いる事で、現実世界の出来事の連続性を再現する事ができるからです。そこに曖昧さはありません。
どんな段階においても、どんな分類をしたとしても、非常に正確です。
真実か、誤りか。それだけです。
In the box or outside the box.
It’s very clear, ultimate precision.
And that is why mathematics is so powerful and being used more often right through to sex.
仮定が当てはまるかどうか。
とても明確です。究極の正確性です。
だから数学はとても強力で、セックスにも用いることができるのです。
(12:00)
And that’s why it’s so hard because you’re using the limits of our evolution right to their extreme.
We’re using, we’re taming those innate sensations with the most ultimate precision we can.
セックスに数学を使う事はそんなに難しい事ではありません。なぜなら進化の力を極限まで使う事ができるからです。
可能な限りの最高の正確性で、私たちは本能を制御して利用することができます。
(字幕では”And that’s why it’s so hard”となっていましたが、演者の意図の理解が困難だったため、日本語訳では”not so hard”に変えました。)
9.「数学」と世界平和
You see, mathematics as you can see, it’s just what’s so breathtaking is that it emerged independently across the globe.
And when people came together in peace or war they may have clashed when it came to religion, cultures, languages,
but their mathematics, or pure pattern recognition just meshed.
数学の最も驚嘆すべき点は、それは地球上で全く別々の所から同時に発生したという事です。
人々は、宗教や文化や言語に関する衝突から、戦争や平和を繰り返しててきました。
しかし数学は、または純粋なパターン認識は、調和する事ができます。
You see mathiematics lies right at the roots of humanity.
Like sex, it transcends human culture.
And now that I’ve shared that with you, you are the sexiest ladies in town.
(laughter)
Thank you very much.
数学は全ての人間性の根幹です。
セックスのように、人間の文化を進歩させてきました。
さて、この話を共有した今、皆さんはこの町で一番セクシーな女性たちです。
(会場笑)
どうもありがとうございました。
